题目内容
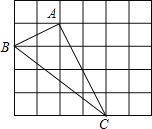
【题目】在四边形ABCD中，
，
，
．
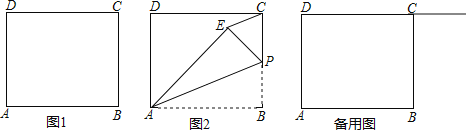
为边BC上一点，将
沿直线AP翻折至
的位置
点B落在点E处
如图1，当点E落在CD边上时，利用尺规作图，在图1中作出满足条件的图形不写作法，保留作图痕迹，用2B铅笔加粗加黑
并直接写出此时
______；
如图2，若点P为BC边的中点，连接CE，则CE与AP有何位置关系？请说明理由；
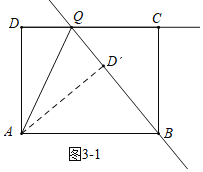
点Q为射线DC上的一个动点，将
沿AQ翻折，点D恰好落在直线BQ上的点
处，则
______；
【答案】（1）①6；②结论：
（2）为4和16．
【解析】
如图1中，以A为圆心AB为半径画弧交CD于E，作
的平分线交BC于点P，点P即为所求
理由勾股定理可得DE．
如图2中，结论：
只要证明
，
即可解决问题．
分两种情形分别求解即可解决问题．
解：如图1中，以A为圆心AB为半径画弧交CD于E，作
的平分线交BC于点P，点P即为所求．
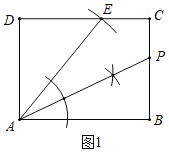
在
中，
，
，
，
，
故答案为6．
如图2中，结论：
．
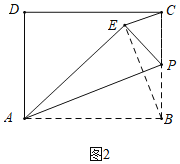
理由：由翻折不变性可知：
，
，
垂直平分线段BE，
即
，
，
，
，
．
如图
中，当点Q在线段CD上时，设
．
在
中，
，
，
，
，
在
中，
，
，
，
．
如图
中，当点Q在线段DC的延长线上时，
，
，
，
，
，
在
中，
，
，
综上所述，满足条件的DQ的值为4或16．
故答案为4和16．
练习册系列答案
名校通行证有效作业系列答案
相关题目
