Question

【题目】过的顶点的两条直线分三角形边上的中线所成的比，则这两条直线分边所成的比为（ ）

A. 4:5:3 B. 3:4:2 C. 2:3:1 D. 1:1:1

Answer 1

【答案】B

【解析】

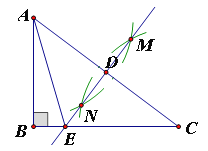
根据AD是中线得点D是中点，过点D作DM∥AC交BG、BH于点N、M，则N、M也是边BG与边BH的中点，然后根据平行线分线段成比例定理列式求出AG与AC的关系，CH与AC的关系，再求出GH与AC的关系，然后即可求出AG：GH：HC的比值．

如图，过点D作DM∥AC交BG、BH于点N、M，

∴，，

∵AE：EF：FD=4：3：1，

∴，，

∴DN=AG，DM=AH，

又∵AD是△ABC的中线，

∴点D是BC的中点，

∴点N是BG的中点，点M是BH的中点，

∴DN=CG，DM=CH，

∴AG=CG，CH=AH，

∵AG+CG=AC，CH+AH=AC，

∴AG=AC，CH=AC，

∴GH=AC-AG-CH=AC-AC-AC=AC，

∴AG：GH：HC=AC：AC：AC=3：4：2．

故选B．