Question

【题目】【阅读】
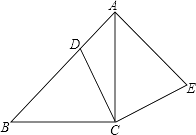
如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．

（1）【理解】
若点D与点A重合，则这个操作过程为FZ[ ， ]；
（2）【尝试】
若点D恰为AB的中点（如图2），求θ；

（3）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；
（4）【探究】
经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]．

Answer 1

【答案】
（1）45°；3
（2）

解：如答图1所示，若点D恰为AB的中点，连接CD并延长交x轴于点F．证明△BCD≌△AFD，进而得到△OCD为等边三角形，则θ=30°；

（3）

解：经过FZ[45°，a]操作，点B落在点E处，则点D落在x轴上，AB⊥直线l，

如答图2所示：

若点E在四边形0ABC的边AB上，

由折叠可知，OD=OC=3，DE=BC=2．

∵AB⊥直线l，θ=45°，

∴△ADE为等腰直角三角形，

∴AD=DE=2，

∴OA=OD+AD=3+2=5，

∴a=5；

由答图2可知，当0＜a＜5时，点E落在四边形0ABC的外部．

（4）

解：FZ[30°，2+ ]，FZ[60°，2+3 ]．

如答图3、答图4所示．

【解析】解：（1）【理解】
若点D与点A重合，由折叠性质可知，OA=OC=3，θ= ∠AOC=45°，
∴FZ[45°，3]．
【考点精析】通过灵活运用翻折变换（折叠问题），掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．