题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. 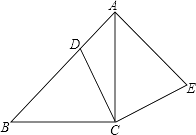
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
【答案】
(1)证明:∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴∠DCE=90°,CD=CE,
∵∠ACB=90°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中
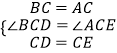 ,
,
∴△BCD≌△ACE,
∴∠B=∠CAE=45°,
∴∠BAE=45°+45°=90°,
∴AB⊥AE;
(2)证明:∵BC2=ADAB,
而BC=AC,
∴AC2=ADAB,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,
∴四边形ADCE为矩形,
∵CD=CE,
∴四边形ADCE为正方形.
【解析】(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
【考点精析】关于本题考查的等腰直角三角形和正方形的判定方法,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案