题目内容
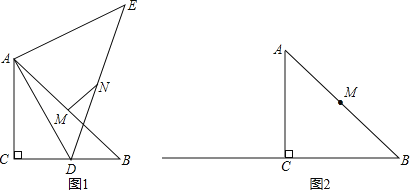
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
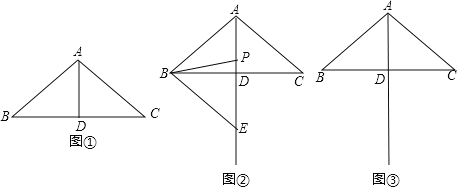
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
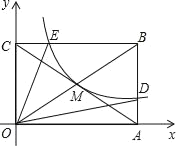
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
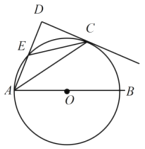
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
【答案】(1)①50![]() ;②
;②![]() ;(2)
;(2)![]() ;(3)AE的最小值
;(3)AE的最小值![]() .
.
【解析】
(1)①利用等腰三角形的性质即可解决问题.②证明![]() ,
,![]() ,推出
,推出![]() 即可.
即可.
(2)如图③中,以P为圆心,PB为半径作⊙P.利用圆周角定理证明![]() 即可解决问题.
即可解决问题.
(3)因为点E在射线CE上运动,点P在线段AD上运动,所以当点P运动到与点A重合时,AE的值最小,此时AE的最小值![]() .
.
(1)①如图②中,

∵![]() ,
,![]() ,
,
∴![]() ,
,
②结论:![]() .
.
理由:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AE垂直平分线段BC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为50,![]() .
.
(2)如图③中,以P为圆心,PB为半径作⊙P.
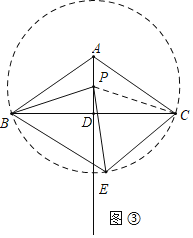
∵AD垂直平分线段BC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ![]() .
.
(3)如图④中,作![]() 于H,
于H,
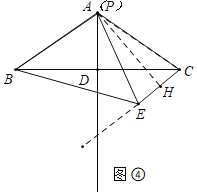
∵点E在射线CE上运动,点P在线段AD上运动,
∴当点P运动到与点A重合时,AE的值最小,此时AE的最小值![]() .
.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目