题目内容
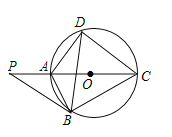
【题目】如图,点P是圆O直径CA延长线上的一点,PB切圆O于点B,点D是圆上的一点,连接AB,AD,BD,CD,PB=BC.
(1)求证:OP=2OC;
(2)若OC=5,sin∠DCA=![]() ,求BD的长.
,求BD的长.
【答案】(1)见解析;(2)4+3![]()
【解析】
(1)连接OB,由切线的性质和等腰三角形的性质得出得出∠P=30°,再由直角三角形的性质即可得出结论;
(2)作AH⊥BD于H,由圆周角定理和三角函数得出AC=10,CD=8,AD=6,由直角三角形的性质得出AB=![]() AC=5,由三角函数得出AH=3,BH=4,求出DH=
AC=5,由三角函数得出AH=3,BH=4,求出DH=![]() AH=3
AH=3![]() ,即可得出结果.
,即可得出结果.
(1)证明:如图1,连接OB,
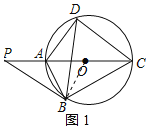
∵PB切圆O于点B,
∴∠OBP=90°,
∴∠P+∠POB=90°,
∵OB=OC,
∴∠OBC=∠OCB,
∴∠POB=∠OBC+∠OCB=2∠OCB,
∵PB=BC,
∴∠P=∠OCB,
∴∠P+∠POB=∠P+2∠OCB=3∠P=90°,
∴∠P=30°,
∴OP=2OB=2OC;
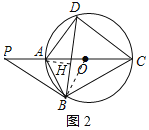
(2)解:如图2,作AH⊥BD于H,
∵AC为⊙O的直径,
∴∠ADC=90°,∠ABC=90°
∵OC=5,sin∠DCA=![]() ,
,
∴AC=10,CD=8,AD=6,
∵∠OCB=30°,
∴AB=![]() AC=5,
AC=5,
∵sin∠ABD=sin∠DCA=![]() ,
,
∴AH=3,BH=4,
∵∠ADH=∠OCB=30°,
∴DH=![]() AH=3
AH=3![]() ,
,
∴BD=BH+DH=4+3![]() .
.

练习册系列答案
相关题目
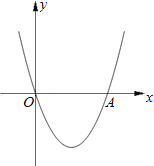
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .