题目内容
【题目】如图,矩形ABCD中,点E在边BC上,EF⊥AE交AD于点F,若AB=2,BC=7,BE=5,则FD的长度为_____.

【答案】![]()
【解析】
首先利用勾股定理计算出AE的长,再证明△ABE∽△FEA,根据相似三角形的性质可得![]() =
=![]() ,代入相应线段的长可得EF的长,在Rt△AEF中,利用勾股定理,即可算出AF的长,进而得到DF的长.
,代入相应线段的长可得EF的长,在Rt△AEF中,利用勾股定理,即可算出AF的长,进而得到DF的长.
解:在△ABE中:AE2=AB2+BE2,
∵AB=2,BE=5,
∴AE=![]() =
=![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AF∥BC,∠B=90°,
∴∠EAF=∠BEA,
∵EF⊥AE,
∴∠AEF=90°,
∵∠EAF=∠BEA,∠B=∠AEF,
∴△ABE∽△FEA,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
EF=![]() ,
,
在Rt△AEF中:AF2=AE2+EF2,
AF2=(![]() )2+(
)2+(![]() )2,
)2,
解得:AF=![]() ,
,
∵BC=7,
∴FD=7﹣![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
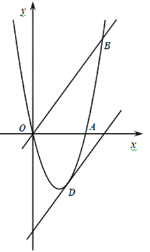
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
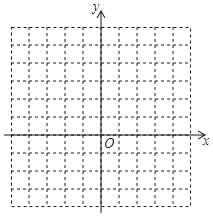
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .