题目内容
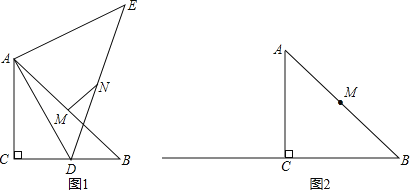
【题目】如图,等腰直角三角形ABC中,∠ACB=90°.D为射线BC上一动点.连接AD,将线段AD绕点A逆时针旋转90°至点E,连接AE、DE.点M、N分别是AB、DE的中点,连接MN.
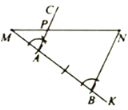
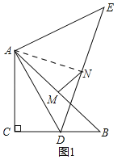
(1)如图1,点D在线段BC上.
①猜想MN与AB的位置关系,并证明你的猜想;
②连接EB,猜想BE与BC的位置关系;
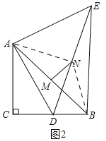
(2)在图2中,若点D在线段BC的延长线上,BE与BC的位置关系是否改变?请你补全图形后,证明你的猜想.
【答案】(1)①垂直,证明见解析;②垂直,理由见解析;(2)垂直,理由见解析.
【解析】
(1)①先判断出AD=![]() AN,AC=
AN,AC=![]() AM,进而得出
AM,进而得出![]() ,判断出△CAD∽△MAN,即可得出结论;
,判断出△CAD∽△MAN,即可得出结论;
②先判断出MN是AB的中垂线,得出AN=BN,再判断出AN=DN=EN=![]() DE,进而得出DN=EN=BN,最后用三角形的内角和即可得出结论;
DE,进而得出DN=EN=BN,最后用三角形的内角和即可得出结论;
(2)分两种情况,同(1)②的方法,即可得出结论.
(1)①垂直,
理由:如图1,
由旋转知,AD=AE,∠DAE=90°,
∵点N是DE的中点,
∴∠DAN=∠![]() ∠DAE=45°,∠AND=90°,
∠DAE=45°,∠AND=90°,
∴AD=![]() AN,
AN,
∴![]() =
=![]() ,
,
在等腰直角三角形ABC中,∠ACB=90°,
∴∠BAC=45°,AB=![]() AC,
AC,
∵M是AB的中点,
∴AM=![]() AB=
AB=![]() AC,
AC,
∴AC=![]() AM,
AM,
∴![]() ,
,
∴![]() ,
,
∵∠DAN=∠BAC=45°,
∴∠CAD=∠MAN,
∴△CAD∽△MAN,
∴∠AMN=∠ACD=90°,
∴MN⊥AB;
②垂直;
理由:如图2,
连接AB,BN,由①知,MN⊥AB,
∵M是AB的中点,
∴MN是AB的中垂线,
∴AN=BN,
由旋转知,AD=AE,∠DAE=90°,
∴点N是DE的中点,
∴AN=DN=EN=![]() DE,
DE,
∴DN=EN=BN,
∴∠BDN=∠DBN,∠BEN=∠EBN,
∵∠BDE+∠BED+∠DBE=180°,
∴∠BDN+∠BEN+∠DBN+∠EBN=2∠DBN+2∠EBN=2(∠DBN+∠EBN)=2∠DBE=180°,
∴∠DBE=90°,
∴BE⊥BC;
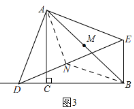
(2)关系不改变,DE⊥BC,
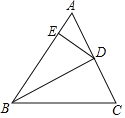
理由:当CD<AC时,如图3,
同(1)②的方法;
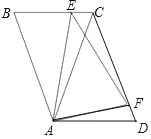
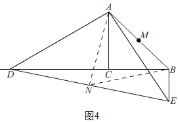
当CD>AC时,如图4,
同(1)②的方法.

 名校课堂系列答案
名校课堂系列答案【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
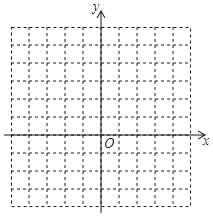
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .