题目内容
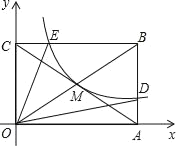
【题目】如图,反比例函数![]() (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.若四边形ODBE的面积为6,则k的值为_____.
【答案】2
【解析】
设M点坐标为(a,b),则k=ab,即y=![]() ,然后根据矩形性质得出A(2a,0),C(0,2b),B(2a,2b),从而进一步可以得出D点、E点各自坐标,最后利用S矩形OABC=S△OAD+S△OCE+S四边形ODBE建立方程求解即可.
,然后根据矩形性质得出A(2a,0),C(0,2b),B(2a,2b),从而进一步可以得出D点、E点各自坐标,最后利用S矩形OABC=S△OAD+S△OCE+S四边形ODBE建立方程求解即可.
解:设M点坐标为(a,b),则k=ab,即y=![]() ,
,
∵点M为矩形OABC对角线的交点,
∴A(2a,0),C(0,2b),B(2a,2b),
∴D点的横坐标为2a,E点的纵坐标为2b,
又∵点D、点E在反比例函数y=![]() 的图象上,
的图象上,
∴D点的纵坐标为![]() b,E点的横坐标为
b,E点的横坐标为![]() a,
a,
∵S矩形OABC=S△OAD+S△OCE+S四边形ODBE,
∴2a2b=![]() 2a
2a![]() b+
b+![]() 2b
2b![]() a+6,
a+6,
∴ab=2,
∴k=2.
故答案为2.

练习册系列答案
相关题目
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .