题目内容
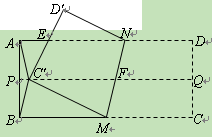
如图所示,正方形A BCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.
BCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.

求证:△BCG≌△DCE;
(1)求证:BH⊥DE;
(2)试问当CG等于多少时,BH垂直平分DE?
 BCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.
BCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H.
求证:△BCG≌△DCE;
(1)求证:BH⊥DE;
(2)试问当CG等于多少时,BH垂直平分DE?
解:(1) ∵ 四边形ABCD和四边形GCEF均为正方 形
形
∴ BC = DC,CG = CE,∠BCG =∠DCE = 90
∴ △BCG≌△DCE
(2) ∵ △BCG≌△DCE
∴ ∠GBC =∠EDC
又 ∵∠EDC +∠CED = 90
∴ ∠BHE = 90 ,即BH⊥DE
,即BH⊥DE
(3) 连结B D,由 (2) 知BH⊥DE
D,由 (2) 知BH⊥DE

要使BH垂直平分DE,则必满足条件BD = BE
∵ 四边形ABCD是边长为1的正方形
∴ BE =" DB" =
又 ∵ 四边形GCEF是正方形
∴
即当 时,BH垂直平分DE
时,BH垂直平分DE
 形
形∴ BC = DC,CG = CE,∠BCG =∠DCE = 90

∴ △BCG≌△DCE
(2) ∵ △BCG≌△DCE
∴ ∠GBC =∠EDC
又 ∵∠EDC +∠CED = 90

∴ ∠BHE = 90
 ,即BH⊥DE
,即BH⊥DE(3) 连结B
 D,由 (2) 知BH⊥DE
D,由 (2) 知BH⊥DE
要使BH垂直平分DE,则必满足条件BD = BE
∵ 四边形ABCD是边长为1的正方形
∴ BE =" DB" =

又 ∵ 四边形GCEF是正方形
∴

即当
 时,BH垂直平分DE
时,BH垂直平分DE略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

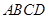 的顶点
的顶点 作直线
作直线 ,过
,过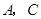 作
作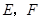 .若
.若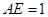 ,
,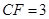 ,则
,则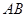 的长度为 .
的长度为 .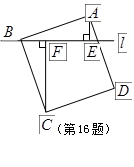

 ,
, .
.
 ,求梯形ABCD的面积
,求梯形ABCD的面积