题目内容
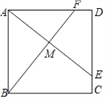
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,动点P从点D出发,沿射线
,动点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段
的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段![]() 上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
上以每秒1个单位长的速度向点B运动,点P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,运动时间为t(秒)
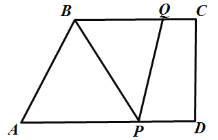
(1)设![]() 的面积为S,求S与t之间的函数关系式;
的面积为S,求S与t之间的函数关系式;
(2)若四边形![]() 为平行四边形,求运动时间t;
为平行四边形,求运动时间t;
(3)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?
【答案】(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3) ![]() 或者t=3.6
或者t=3.6
【解析】
(1) 根据![]() 可得
可得![]() ,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
,再根据三角形面积的求法,求出S与t之间的函数关系式即可;
(2)根据平行四边形的判定定理得到AP=BQ时四边形ABQP是平行四边形,再求出t即可得到答案;
(3)根据题意分三种情况(PB=PQ,PQ=BQ,PB=BQ),再根据等腰三角形的性质,分类讨论求出t即可得到答案;
解:(1) ∵BC=20,动点Q以每秒1个单位长的速度向点B运动,点P从点D出发,沿射线![]() 的方向以每秒2个单位长的速度运动,
的方向以每秒2个单位长的速度运动,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴CD的长度是![]() 以BQ为底边的高的长度,
以BQ为底边的高的长度,
∴![]() ;
;
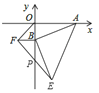
(2)如下图:

由题意得:![]() ,
,![]() ,
,
∵![]() ,
,
∴当AP=BQ时,四边形ABQP是平行四边形(一组对边平行且相等的四边形是平行四边形),
即:![]() ,
,
解得:![]() ;
;
(3)情况1:如下图:作PN⊥BC与点N,

当PB=PQ时,
NQ=BN(三线合一定理),
∵NQ=PD-CQ=2t-t=t,
∴BN=t,BQ=2t,
∵BC-BQ=CQ
∴20-2t=t,
解得:![]() ;
;
情况2:如图,作PN⊥BC与点N,

当PQ=BQ时,
NQ=PD-CQ=2t-t=t,
PQ=BQ=20-t,
在直角三角形NPQ中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
解得t=3.6;
情况3:如图,

当PB=BQ时,
BN=20-2t,
BP=BQ=20-t,
在直角三角形BNP中,
![]() (勾股定理),
(勾股定理),
∴![]() ,
,
整理得:![]()
![]() ,
,
故方程无解,综上可得:![]() 或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.
或者t=3.6时,以B、P、Q三点为顶点的三角形是等腰三角形.