题目内容
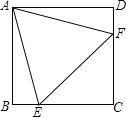
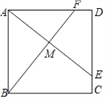
【题目】如图，正方形ABCD中，E、F分别是边CD、DA上的点，且CE=DF，AE与BF交于点M．求证：AE⊥BF．
【答案】证明见解析.
【解析】试题分析：首先证明△ABF≌△DAE（SAS），即可推出∠AFB=∠DEA，由∠D=90°，推出∠DEA+∠DAE=90°，推出∠AFB+∠DAE=90°，推出∠AMF=180°-90°=90°．
试题解析：证明：∵四边形ABCD是正方形，
∴∠BAD=∠ADE=90°，AD=AB=DC，
∵DF=CE，
∴AF=DE，
∵在△ABF和△DAE中，
，
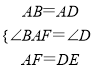∴△ABF≌△DAE（SAS）；
∴∠AFB=∠DEA，
∵∠D=90°，
∴∠DEA+∠DAE=90°，
∴∠AFB+∠DAE=90°，
∴∠AMF=180°﹣90°=90°，
∴AE⊥BF．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
