题目内容
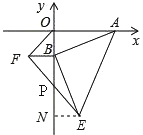
【题目】如图,点A的坐标为(8,0),点B为y轴负半轴上的一动点,分别以OB,AB为直角边在第三、第四象限作等腰直角三角形OBF,等腰直角三角形ABE,连接EF交y轴与P点,当点B在y轴上移动时,则PB的长度是( )
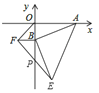
A.2B.4C.不是已知数的定值D.PB的长度随点B的运动而变化
【答案】B
【解析】
作EN⊥y轴于N,求出∠NBE=∠BAO,证△ABO≌△BEN,求出∠OBF=∠FBP=∠BNE=90°,证△BFP≌△NEP,推出BP=NP,即可得出答案.
解:如图,作EN⊥y轴于N,
∵∠ENB=∠BOA=∠ABE=90°,
∴∠OBA+∠NBE=90°,∠OBA+∠OAB=90°,
∴∠NBE=∠BAO,
在△ABO和△BEN中,
 ,
,
∴△ABO≌△BEN(AAS),
∴OB=NE=BF,
∵∠OBF=∠FBP=∠BNE=90°,
在△BFP和△NEP中,
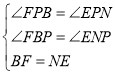 ,
,
∴△BFP≌△NEP(AAS),
∴BP=NP,
又∵点A的坐标为(8,0),
∴OA=BN=8,
∴BP=NP=4,
故选:B.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目