Question

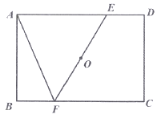
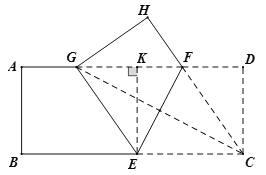
【题目】如图，将矩形纸片（）折叠，使点刚好落在线段上，且折痕分别与边，相交于点，，设折叠后点，的对应点分别为点，.

（1）判断四边形的形状，并证明你的结论；

（2）若，且四边形的面积，求线段的长.

Answer 1

【答案】（1）四边形为菱形，理由见解析；（2）

【解析】

（1）根据折叠的性质可得EC=EG，GF=CF，，由GF∥EC，可得，进一步可得GE=GF，于是可得结论；

（2）根据题意可先求得CE的长，过点E作EK⊥GF于点K，在Rt△GEK中，根据勾股定理可求得GK的长，于是FK可求，在Rt△EFK中，再利用勾股定理即可求得结果.

（1）四边形为菱形，理由如下：

证明：由折叠可得：，，，

又∵，

∴，

∴，

∴，

∴，

∴四边形为菱形.

（2）如图，∵四边形为菱形，且其面积为，∴，

∴，

过点E作EK⊥GF于点K，则EK=AB=4，

在Rt△GEK中，由勾股定理得：，

∴，

在Rt△EFK中，由勾股定理得：.