Question

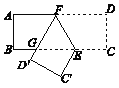
【题目】已知在矩形ABCD中，点E在边BC上，BE＝2CE，将矩形沿着过点E的直线翻折后，点C，D分别落在边BC下方的点C′，D′处，且点C′，D′，B在同一条直线上，折痕与边AD交于点F，D′F与BE交于点G. 当AB＝5时，△EFG的周长为_________________.

Answer 1

【答案】10

【解析】根据翻折的性质可得CE=C′E，再根据直角三角形30°角所对的直角边等于斜边的一半判断出∠EBC′=30°，然后求出∠BGD′=60°，根据对顶角相等可得∠FGE=∠BGD′=60°，根据两直线平行，内错角相等可得∠AFG=∠FGE，再求出∠EFG=60°，然后判断出△EFG是等边三角形，根据等边三角形的性质表示出EF，即可得解．

如图，

由翻折的性质得，CE=C′E，

∵BE=2CE，

∴BE=2C′E，

又∵∠C′=∠C=90°，

∴∠EBC′=30°，

∵∠FD′C′=∠D=90°，

∴∠BGD′=60°，

∵AD∥BC，

∴∠AFG=∠FGE=60°，

∴∠EFG=（180°-∠AFG）=（180°-60°）=60°，

∴△EFG是等边三角形，

∵AB=5，

∴EF=5÷=，

∴△EFG的周长=3×=10．

故答案为：10．