题目内容
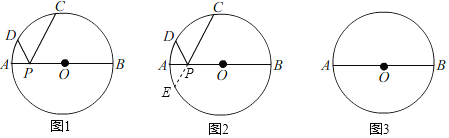
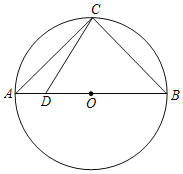
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,![]() ,点D是AB上一点(点D与A,B不重合),连接CD.
,点D是AB上一点(点D与A,B不重合),连接CD.
(1)用尺规作图,线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE;(保留作图痕迹,不写作法.)
(2)当AD=BF时,求∠BEF的度数.
(3)求证:AD2+BD2=2CD2.
【答案】(1)如图,见解析;CE、BE为所作;(2)∠BEF=67.5°;(3)见解析.
【解析】
(1)延长线段DC,以C为圆心,以适当的长为半径画弧交CD于两点M、N.2)分别以两点为圆心,以大于二分之一MN同样长为半径画弧,两弧交于P,作射线CP,以C为圆心,以CD长为半径作弧,交射线CP与点E,连接BE即可.
(2)根据圆中,直径对直角推导出,△ACB为等腰直角三角形,根据旋转的性质得到,CD=CE,∠ACD=∠BCE,由此判断呢△ACD≌△BCE,得到∠CBE=∠A=45°,再根据AD=BF推出∠BEF=∠BFE,最后计算∠BEF的度数即可.
(3)根据勾股定理可得BE2+DB2=DE2,根据题意和直角三角形的边角关系可得BE=AD,DE=![]() CD,然后换算解决即可.
CD,然后换算解决即可.
(1)解:如图,CE、BE为所作;
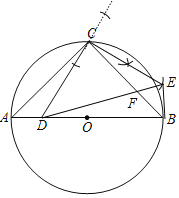
(2)解:∵AB为直径,
∴∠ACB=90°,
∵![]() ,
,
∴AC=BC,
∴△ACB为等腰直角三角形,
∴∠A=∠ABC=45°,
∵线段CD绕点C按逆时针方向旋转90°得到线段CE,
∴∠DCE=90°,CD=CE,
∴∠ACD=∠BCE,
在△ACD和△BCE中
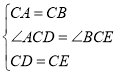 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CBE=∠A=45°,
∵AD=BF,
∴BF=BE,
∴∠BEF=∠BFE,
∴∠BEF=![]() (180°﹣45°)=67.5°;
(180°﹣45°)=67.5°;
(3)证明:∵∠ABC=45°,∠CBE=45°,
∴∠DBE=90°,
∴BE2+DB2=DE2,
∵BE=AD,DE=![]() CD,
CD,
∴AD2+BD2=2CD2.