题目内容
某公司销售一种进价为20元/个的计算机,其销售量y(万个)与销售价格x(元/个)的变化如下表:
同时,销售过程中的其他开支(不含造价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)观察并分析表中的y与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识写出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净得利润z(万个)与销售价格x(元/个)的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
(3)该公司要求净得利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元?
解:(1)根据表格中数据可得出:y与x是一次函数关系,设解析式为:y=ax+b,
则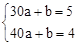 ,解得:
,解得: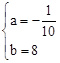 。
。
∴函数解析式为:y= x+8。
x+8。
(2)根据题意得:
z=(x﹣20)y﹣40=(x﹣20)( x+8)﹣40=
x+8)﹣40= x2+10x﹣200=
x2+10x﹣200= (x2﹣100x)﹣200
(x2﹣100x)﹣200
= [(x﹣50)2﹣2500]﹣200=
[(x﹣50)2﹣2500]﹣200= (x﹣50)2+50,
(x﹣50)2+50,
∵ <0,∴x=50,z最大=50。
<0,∴x=50,z最大=50。
∴该公司销售这种计算器的净得利润z与销售价格x)的函数解析式为z= x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。
x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。
(3)当公司要求净得利润为40万元时,即 (x﹣50)2+50=40,解得:x1=40,x2=60。
(x﹣50)2+50=40,解得:x1=40,x2=60。
作函数图象的草图,

通过观察函数y= (x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
而y与x的函数关系式为:y= x+8,y随x的增大而减少,
x+8,y随x的增大而减少,
∴若还需考虑销售量尽可能大,销售价格应定为40元/个。
则
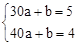 ,解得:
,解得: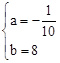 。
。∴函数解析式为:y=
 x+8。
x+8。(2)根据题意得:
z=(x﹣20)y﹣40=(x﹣20)(
 x+8)﹣40=
x+8)﹣40= x2+10x﹣200=
x2+10x﹣200= (x2﹣100x)﹣200
(x2﹣100x)﹣200=
 [(x﹣50)2﹣2500]﹣200=
[(x﹣50)2﹣2500]﹣200= (x﹣50)2+50,
(x﹣50)2+50,∵
 <0,∴x=50,z最大=50。
<0,∴x=50,z最大=50。∴该公司销售这种计算器的净得利润z与销售价格x)的函数解析式为z=
 x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。
x2+10x﹣200,销售价格定为50元/个时净得利润最大,最大值是50万元。(3)当公司要求净得利润为40万元时,即
 (x﹣50)2+50=40,解得:x1=40,x2=60。
(x﹣50)2+50=40,解得:x1=40,x2=60。作函数图象的草图,

通过观察函数y=
 (x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.
(x﹣50)2+50的图象,可知按照公司要求使净得利润不低于40万元,则销售价格的取值范围为:40≤x≤60.而y与x的函数关系式为:y=
 x+8,y随x的增大而减少,
x+8,y随x的增大而减少,∴若还需考虑销售量尽可能大,销售价格应定为40元/个。
试题分析:(1)根据数据得出y与x是一次函数关系,进而利用待定系数法求一次函数解析式。
(2)根据z=(x﹣20)y﹣40得出z与x的函数关系式,应用二次函数最值原理求解即可。
(3)首先求出40=
 (x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果。
(x﹣50)2+50时x的值,从而二次函数的性质根据得出x(元/个)的取值范围,结合一次函数的性质即可求得结果。 
练习册系列答案
相关题目

 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,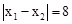 。
。
 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。 经过A、C两点,与x轴的另一个交点是点D,连接BD.
经过A、C两点,与x轴的另一个交点是点D,连接BD.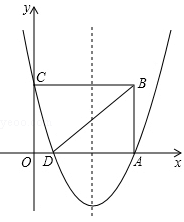
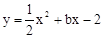 的图象过C点.
的图象过C点.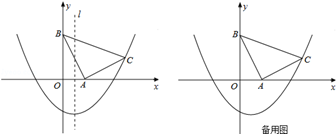


 B.
B.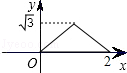 C.
C. D.
D.
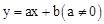 、二次函数
、二次函数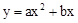 和反比例函数
和反比例函数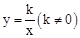 在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】
在同一直角坐标系中图象如图,A点为(-2,0)。则下列结论中,正确的是【 】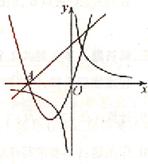
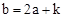
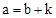
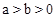
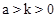
 图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(
图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ,y2)是抛物线上两点,则
,y2)是抛物线上两点,则