题目内容
【题目】已知在平面直角坐标系中,O为坐标原点,点A的坐标为(1,a),点B的坐标为(b,1),点C的坐标为(c,0),其中a、b满足(a+b﹣8)2+|a﹣b+2|=0.
(1)求A、B两点的坐标;
(2)当△ABC的面积为6时,求点C的坐标;
(3)当4≤S△ABC≤10时,求点C的横坐标c的取值范围.
【答案】(1)A(1,3),B(5,1);(2)(1,0)或(13,0);(3)﹣3≤c≤3或11≤c≤17.
【解析】
(1)利用非负数的性质,把问题转化为方程组解决即可;
(2)分两种情形画出图形,分别构建方程即可解决问题;
(3)分两种情形分别构建不等式即可解决问题;
(1)∵(a+b﹣8)2+|a﹣b+2|=0.
∴![]() ,
,
解得![]() ,
,
∴A(1,3),B(5,1);
(2)①如图1中,当点C在直线AB的下方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
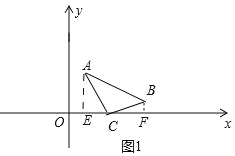
∵S△ABC=S四边形AEFB﹣S△AEC﹣S△BCF=![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×1×(5﹣c)=7﹣c,
×1×(5﹣c)=7﹣c,
∴7﹣c=6
解得c=1.
②如图2中,当点C在直线AB的上方时,作AE⊥x轴于E,BF⊥x轴于F.设C(c,0).
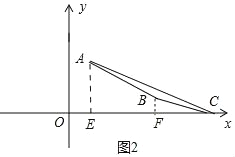
∵S△ABC=S△AEC﹣S四边形AEFB﹣S△BCF=![]() ×3×(c﹣1)﹣
×3×(c﹣1)﹣![]() ×(1+3)×4﹣
×(1+3)×4﹣![]() ×1×(c﹣5)=c﹣7,
×1×(c﹣5)=c﹣7,
∴c﹣7=6,
解得c=13,
∴满足条件的点C坐标为(1,0)或(13,0).
(3)由(2)可知,当点C在直线AB下方时,S△ABC=7﹣c,
∴4≤7﹣c≤10,
∴﹣3≤c≤3,
当点C在直线AB是上方时,S△ABC=c﹣7,
∴4≤c﹣7≤10,
∴11≤c≤17,
所以满足条件的c的取值范围为﹣3≤c≤3或11≤c≤17.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目