题目内容
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径.PC是⊙O的切线,C为切点,PD⊥AB于点D,交AC于点E.
(1)求证:∠PCE=∠PEC;
(2)若AB=10,ED=![]() , sinA=
, sinA=![]() , 求PC的长.
, 求PC的长.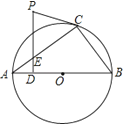
【答案】解:(1)∵PC是圆O的切线,
∴∠PCA=∠B.
∵AB是圆O的直径,
∴∠ACB=90°.
∴∠A+∠B=90°.
∵PD⊥AB,
∴∠A+∠AED=90°.
∴∠AED=∠B.
∵∠PEC=∠AED,
∴∠PCE=∠PEC.
(2)如图所示,过点P作PF⊥AC,垂足为F.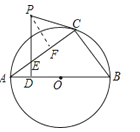
∵AB=10,sinA=![]() ,
,
∴BC=AB![]() =6.
=6.
∴AC=![]() =8.
=8.
∵DE=![]() ,sinA=
,sinA=![]() ,
,
∴AE=![]() .
.
∴EC=AC﹣AE=8﹣![]() =
=![]() .
.
∵PC=PE,PF⊥EC,
∴EF=![]() .
.
∵∠AED=∠PEF,∠EDA=∠EFP,
∴△AED∽△PEF.
∴![]() ,
,![]() .
.
解得:EP=![]() .
.
∴PC=![]() .
.
【解析】(1)由弦切角定理可知∠PCA=∠B,由直角所对的圆周角等于90°可知∠ACB=90°.由同角的余角相等可知∠AED=∠B,结合对顶角的性质可知∠PCE=∠PEC;
(2)过点P作PF⊥AC,垂足为F.由锐角三角函数的定义和勾股定理可求得AC=8,AE=![]() , 由等腰三角形三线合一的性质可知EF=
, 由等腰三角形三线合一的性质可知EF=![]() , 然后证明△AED∽△PEF,由相似三角形的性质可求得PE的长,从而得到PC的长.
, 然后证明△AED∽△PEF,由相似三角形的性质可求得PE的长,从而得到PC的长.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目