题目内容
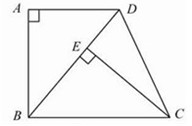
已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)直接写出线段EG与CG的数量关系;
(2)将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明.
(3)将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?(不要求证明)


(1)直接写出线段EG与CG的数量关系;
(2)将图1中△BEF绕B点逆时针旋转45º,如图2所示,取DF中点G,连接EG,CG.你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明.
(3)将图1中△BEF绕B点旋转任意角度,如图3所示,再连接相应的线段,问(1)中的结论是否仍然成立?(不要求证明)



解:(1)CG=EG
(2)(1)中结论没有发生变化,即EG=CG.
证明:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.

在△DAG与△DCG中,
∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.
∴ AG=CG.
在△DMG与△FNG中,
∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.
∴ MG=NG
在矩形AENM中,AM=EN.
在Rt△AMG 与Rt△ENG中,
∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.
∴ AG=EG
∴ EG=CG.
(3)(1)中的结论仍然成立.

(2)(1)中结论没有发生变化,即EG=CG.
证明:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.

在△DAG与△DCG中,
∵ AD=CD,∠ADG=∠CDG,DG=DG,
∴ △DAG≌△DCG.
∴ AG=CG.
在△DMG与△FNG中,
∵ ∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,
∴ △DMG≌△FNG.
∴ MG=NG
在矩形AENM中,AM=EN.
在Rt△AMG 与Rt△ENG中,
∵ AM=EN, MG=NG,
∴ △AMG≌△ENG.
∴ AG=EG
∴ EG=CG.
(3)(1)中的结论仍然成立.

本题主要是利用正方形的性质和三角形全等来证明线段相等。难点在于正确的做出辅助线。

练习册系列答案
相关题目




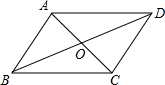
 ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )