题目内容
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，D是AB上一动点，过点D作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是（ ）
A.5
B.4.8
C.4.6
D.4.4
【答案】B
【解析】解：如图，连接CD．
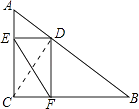
∵∠ACB=90°，AC=6，BC=8，
∴AB= 
=10，
∵DE⊥AC，DF⊥BC，∠C=90°，
∴四边形CFDE是矩形，
∴EF=CD，
由垂线段最短可得CD⊥AB时，线段EF的值最小，
此时，S△ABC= 
BCAC= ABCD，
即 ×8×6= ×10CD，
解得CD=4.8，
∴EF=4.8．
所以答案是：B．
【考点精析】利用垂线段最短对题目进行判断即可得到答案，需要熟知连接直线外一点与直线上各点的所有线段中，垂线段最短；现实生活中开沟引水，牵牛喝水都是“垂线段最短”性质的应用．
练习册系列答案
相关题目
