Question

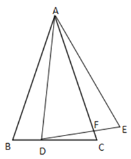
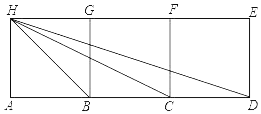
【题目】如图，四边形ABGH、BCFG、CDEF是边长为1的正方形，连接BH、CH、DH，求证：∠ABH+∠ACH+∠ADH＝90°．

Answer 1

【答案】见解析

【解析】

由四边形ABGH，四边形BCFG，四边形CDEF都是正方形，易得＝＝ ，继而可证得△HBC∽△DBH，然后有相似三角形对应角相等，求得∠ACH＝∠DHB，再利用三角形外角的性质求解即可求得答案．

证明：∵四边形ABGH，四边形BCFG，四边形CDEF都是正方形，设边长为a，

则BH＝ ＝a，BC＝a，BD＝2a，

∴＝＝，

又∵∠HBC＝∠DBH（公共角），

∴△HBC∽△DBH，

∴∠ACH＝∠DHB，

∴∠ACH+∠ADH＝∠DHB+∠ADH＝∠ABH＝45°，

∵∠ABH＝45°，

∴∠ABH+∠ACH+∠ADH＝90°．