题目内容
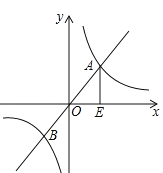
【题目】如图,已知函数y=2x和函数y=![]() 的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则k= ,满足条件的P点坐标是 .
的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B、O、E、P为顶点的四边形是平行四边形,则k= ,满足条件的P点坐标是 .
【答案】8,P1(0,-4),P2(-4,-4),P3(4,4).
【解析】
试题如图
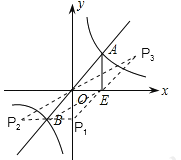
∵△AOE的面积为4,函数y=![]() 的图象过一、三象限,
的图象过一、三象限,
∴S△AOE=![]() OEAE=4,
OEAE=4,
∴OEAE=8,
∴xy=8,
∴k=8,
∵函数y=2x和函数y=![]() 的图象交于A、B两点,
的图象交于A、B两点,
∴2x=![]() ,
,
∴x=±2,
当x=2时,y=4,当x=-2时,y=-4,
∴A、B两点的坐标是:(2,4)(-2,-4),
∵以点B、O、E、P为顶点的平行四边形共有3个,
∴满足条件的P点有3个,分别为:
P1(0,-4),P2(-4,-4),P3(4,4).

练习册系列答案
相关题目