题目内容
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字. 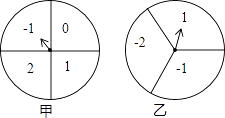
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
【答案】
(1)解:甲盘停止后指针指向数字“1”的概率= ![]()
(2)解:列表得:
转盘A 两个数字之积 转盘B | ﹣1 | 0 | 2 | 1 |
1 | ﹣1 | 0 | 2 | 1 |
﹣2 | 2 | 0 | ﹣4 | ﹣2 |
﹣1 | 1 | 0 | ﹣2 | ﹣1 |
∵由两个转盘各转出一数字作积的所有可能情况有12种,每种情况出现的可能性相同,其中两个数字之积为非负数有7个,负数有5个,
∴P(小华获胜)= ![]() ,P(小明获胜)=
,P(小明获胜)= ![]() .
.
∴这个游戏对双方不公平
【解析】(1)由题意可知转盘中共有四个数,其中“1”只有一种,进而求出其概率;(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与小华、小明获胜的情况,继而求得小华、小明获胜的概率,比较概率大小,即可知这个游戏是否公平.

练习册系列答案
相关题目