题目内容
【题目】如图,OA=OB,∠A=∠B,有下列4个结论:①△AOD≌△BOC,②EA=EB,③点E在∠O的平分线上.④若OC=2CA,△AEC的面积为1,那么四边形OCED的面积为4.其中正确的结论个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
根据全等三角形的判定得出△AOD≌△BOC(ASA),则OD=CO,从而证出△ACE≌△BDE,连接OE,可证明△AOE≌△BOE,则得出点E在∠O的平分线上,根据△AOE≌△BOE、△ACE≌△BDE即可求得S△ACE=S△OCE=S△ODE=S△BDE=1,即可解题.
①在△AOD和△BOC中,
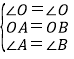 ,
,
∴△AOD≌△BOC(ASA),故①正确;
∴OD=CO,
∴BD=AC,
②在△ACE和△BDE中,
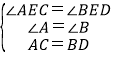 ,
,
∴△ACE≌△BDE(AAS),
∴AE=BE,故②正确;
③连接OE,
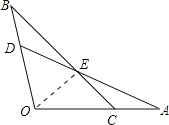
在△AOE和△BOE中,
 ,
,
∴△AOE≌△BOE(SSS),
∴∠AOE=∠BOE,
∴点E在∠O的平分线上,故③正确;
④∵OC=2CA,
∴OD=2BD,
∴S△ACE=S△BDE=1,
∵△AOE≌△BOE,△ACE≌△BDE,
∴S△ODE=2S△BDE=2,
∴四边形OCED的面积为4,故④正确;
故选D.

【题目】某校八年级学生数学科目期末评价成绩是由完成作业、单元检测、期末考试三项成绩构成的,如果期末评价成绩80分以上(含80分),则评为“优秀”.下面表中是小张和小王两位同学的成绩记录:
完成作业 | 单元检测 | 期末考试 | |
小张 | 70 | 90 | 80 |
小王 | 60 | 75 |
(1)若按三项成绩的平均分记为期末评价成绩,请计算小张的期末评价成绩;
(2)若按完成作业、单元检测、期末考试三项成绩按1:2:m的权重,小张的期末评价成绩为81分,则小王在期末(期末成绩为整数)应该最少考多少分才能达到优秀?