题目内容
【题目】证明题：本题须有完整过程，需要括号中的理由，只限本学期所学
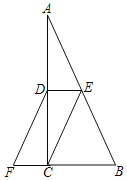
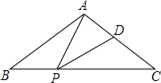
如图，在
中，
是边
上的中线，
，
，
与
交于点
，连接
．
（1）求证：
；
（2）若
，求证：四边形
是菱形．
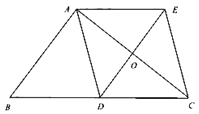
【答案】（1）详见解析；（2）详见解析
【解析】
（1）根据已知条件先判定四边形
为平行四边形，再利用平行四边形的性质和
是边
上的中线可判定四边形
为平行四边形，进而即可得证
；
（2）在（1）的结论基础上只需证得一组邻边相等即可，恰好根据给出的已知条件利用直角三角形斜边上的中线等于斜边的一半即可证得
，从而得证结论．
解：（1）∵
，
∴四边形为平行四边形（平行四边形的定义）
∴
（平行四边形的两组对边分别相等）
∵是边上的中线
∴
∴
又∵
∴四边形为平行四边形（一组对边平行且相等的四边形是平行四边形）
∴
（平行四边形的两组对边分别相等）．
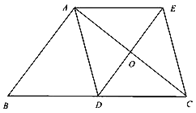
（2）∵
，是边上的中线
∴
由（1）知，四边形为平行四边形
∴四边形是菱形
故答案是：（1）详见解析；（2）详见解析
练习册系列答案
名校课堂系列答案
相关题目
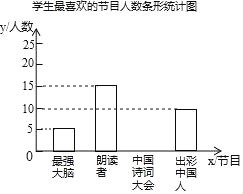
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：根据以上提供的信息，解答下列问题：
节目 | 人数（名） | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
（1）x= ，a= ，b= ；
（2）补全上面的条形统计图；
（3）在喜爱《最强大脑》的学生中，有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动，请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率．
