题目内容
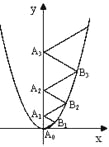
【题目】如图1,矩形AOCB在坐标系中,A、C分别在y轴、x轴的正半轴上,AB>AO,矩形AOCB周长为18,面积为18.
(1)求B点坐标;
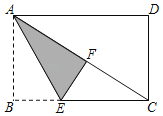
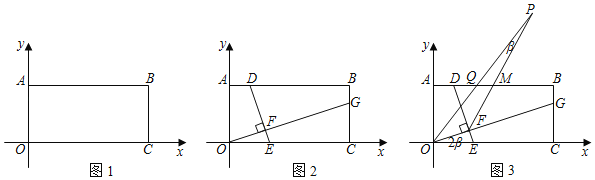
(2)如图2,E、D、G分别在OC、AB、BC上,连接ED、OG,若OG⊥ED于F,OE=2AD,设D点横坐标为t,求CG的长(用含t的代数式表示);
(3)如图3,在(2)的条件下,M是AB中点,连接FM并延长FM至P,连OP交AB于Q,若DQ=![]() ,∠OPF=
,∠OPF=![]() ∠COG=β,求t的值.
∠COG=β,求t的值.
【答案】(1)(6,3);(2)2t;(3)![]()
【解析】
(1)设B点坐标为(m,n),根据矩形周长和面积的值列方程组求解.
(2)作DH⊥OC于H,可证△DHE△OCG,由相似比可得CG=2HE=2AD.
(3)作MN⊥OC于N,交OG于K,连接OD,设DE与OQ交于点R.先证DMKF四点共圆,进而得出∠KFM=45°,再导角推出OP是∠AOG的角平分线,然后可以导出△DRQ和△EOR均为等腰三角形,于是DE的长可用t表示出来.注意到∠AOD与∠NOK相等,可推出OD=DE,最后利用直角三角形AOD列勾股方程解出t的值.
解:(1)设B点坐标为(m,n).
由题意可知:
![]() ,
,
解得:![]() ,
,
∴B点坐标为(6,3).
(2)如图2,作DH⊥OC于H.
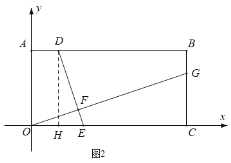
则∠DHE=90°,
∴∠HDE+∠DEH=90°,
∵DH⊥OG于F,
∴∠GOC+∠DEH=∠OFE=90°,
∴∠HDE=∠COG,
∵∠OCG=90°=∠DHE,
∴△DHE△OCG,
∴![]() ,
,
∵B(6,3),
∴AB=OC=6,AO=DH=BC=3,
∴![]() ,
,
∴CG=2HE,
∵D点横坐标为t,
∴OH=AD=t,
∴OE=2AD,
∴HE=OH=t,
∴CG=2HE=2t.
(3)如图3,作MN⊥OC于N,交OG于K,连接OD.
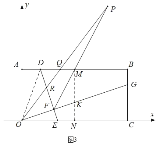
∵M为AB中点,
∴AM=BM=ON=CN=AO=BC=MN=3,KN=![]() CG=t,
CG=t,
∴KN=AD,所以DM=KM,
∵∠DFK=∠DMK=90°,
∴DFKM四点共圆,
∴∠DFM=∠KFM=45°,
∵∠KFM=∠OPF+∠FOP,
∴∠FOP+β=45°,
∴2∠FOP+2β=90°,
∵∠AOC=90°,
∴∠AOQ+∠FOP+∠COG=∠AOQ+∠FOP+2β=90°,
∴∠AOQ=∠FOP,
∵∠OAQ=∠OFR=90°,
∴∠ORF=∠OQA,
∵∠ORF=∠DRQ,∠OQA=∠ROE,
∴∠DRQ=∠OQA,∠ROE=∠ORF,
∴DR=DQ=![]() ,RE=OE=2t,
,RE=OE=2t,
∴DE=DR+RE=![]() +2t,
+2t,
∵tan∠AOD=![]() =
=![]() =tan∠NOK,
=tan∠NOK,
∴∠AOD=∠NOK,
∵∠AOD+∠DOE=∠NOK+∠OEF=90°,
∴∠DOE=∠OEF,
∴OD=DE=![]() +2t,
+2t,
在Rt△AOD中:OA2+AD2=OD2,
∴9+t2=![]() ,
,
解得t=![]() .
.

【题目】为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩.数据如下:
收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88
整理、描述数据:
成绩/分 | 88 | 89 | 90 | 91 | 95 | 96 | 97 | 98 | 99 |
学生人数 | 2 | 1 |
| 3 | 2 | 1 |
| 2 | 1 |
数据样本数据的平均数、众数和中位数如下表
平均数 | 众数 | 中位数 |
93 |
|
|
应用数据
(1)由上表填空:![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________,
________,
(2)根据所给数据,如果该校想确定七年级前![]() 的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
(3)根据数据分析,该校决定在七年级授予测评成绩前![]() 的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.
的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.