题目内容
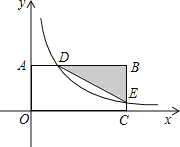
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
的图象与一次函数y=kx+b的图象交于点A,B,点A、B的横坐标分别为1,﹣2,一次函数图象与y轴的交于点C,与x轴交于点D.
(1)求一次函数的解析式;
(2)对于反比例函数y=![]() ,当y<﹣1时,写出x的取值范围;
,当y<﹣1时,写出x的取值范围;
(3)在第三象限的反比例图象上是否存在一个点P,使得S△ODP=2S△OCA?若存在,请求出点P的坐标;若不存在,请说明理由.

【答案】(1)y=x+1;(2)当﹣2<x<0时,y<﹣1;(3)点P的坐标为:(﹣1,﹣2).
【解析】试题分析:(1)由点A.B的横坐标分别为1,2,求得A(1,2),B(2,1),由于点A.B在一次函数y=kx+b的图象上,列方程组即可得到结论;
(2)根据图象即可得到结论;
(3)存在,根据一次函数的解析式得到D(1,0),C(0,1),设P(m,n),根据![]() 列方程即可得到结论.
列方程即可得到结论.
试题解析:(1)∵点A.B的横坐标分别为1,2,
∴y=2,或y=1,
∴A(1,2),B(2,1),
∵点A.B在一次函数y=kx+b的图象上,
∴![]()
∴![]()
∴一次函数的解析式为:y=x+1;
(2)由图象得知:y<1时,写出x的取值范围是2<x<0;
(3)存在,
对于y=x+1,当y=0时,x=1,当x=0时,y=1,
∴D(1,0),C(0,1),
设P(m,n),
![]()
![]()
∴n=2,
∵点P在反比例图象上,
∴m=1,
∴P(1,2).

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?