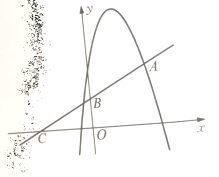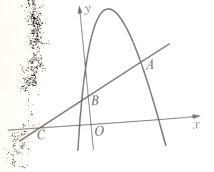题目内容
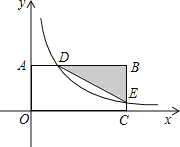
【题目】如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数![]() 的图象分别交BA,BC于点D,E当AD:BD=1:3且
的图象分别交BA,BC于点D,E当AD:BD=1:3且![]() 的面积为18时,则k的值是__________________
的面积为18时,则k的值是__________________
【答案】16
【解析】
首先设B(4a,b),E(4a,d),利用AD:BD=1:3,则D(a,b),进而利用△BDE的面积为18得出ab-ad=12,结合反比例函数图象上的性质得出ab=4ad,进而得出ad的值,即可得出答案.
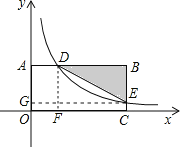
如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
设B(4a,b),E(4a,d).
∵AD:BD=1:3,
∴D(a,b).
又∵△BDE的面积为18,
∴BD=3a,BE=b-d,
∴![]() ×3a(b-d)=18,
×3a(b-d)=18,
∴a(b-d)=12,即ab-ad=12,
∵D,E都在反比例函数图象上,
∴ab=4ad,
∴4ad-ad=12,
解得:ad=4,
∴k=4ad=16.
故答案为:16

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目