题目内容
【题目】如图,正方形ABCD的边长为4cm,E为CD边的中点,,M为AE的中点,过点M作直线分别与AD、BC相交于点P、Q.若PQ=AE,则AP等于__________cm.
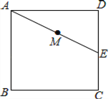
【答案】1.5或2.5
【解析】①过P作PN⊥BC,交BC于点N,如图所示:
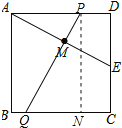
则∠PNQ=∠APN=90°,
∵四边形ABCD为正方形,边长为4cm,E为CD边的中点,
∴AD=DC=PN=4,∠D=90°,DE=2
∴AE=![]() ,
,
在Rt△ADE和Rt△PNQ中,
![]()
∴Rt△ADE≌Rt△PNQ(HL),
∴∠DAE=∠NPQ,
∵∠APQ+∠NPQ=90°,
∴∠APQ+∠DAE=90°,
∴∠AMP=90°,
∵M为AE的中点,
∴AM= ![]() =
=![]() ,
,
∵∠AMP=∠D=90°,∠PAM=∠EAD,
∴△APM∽△AED,
∴![]() ,即
,即![]() ,
,
∴AP=2.5;
②根据对称性得:PD=2.5
AP=AD-PD=4-2.5=1.5;
故答案是:1.5或2.5。

练习册系列答案
相关题目