Question

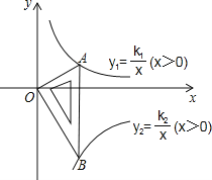
【题目】如图，一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y1=（x＞0）的图象上，顶点B在函数y2=（x＞0）的图象上，∠ABO=30°，求的值．

Answer 1

【答案】

【解析】

设AC=a，则OA=2a，OC=a，根据直角三角形30°角的性质和勾股定理分别计算点A和B的坐标，写出A和B两点的坐标，代入解析式求出k1和k2的值，即可求的值．

设AB与x轴交点为点C

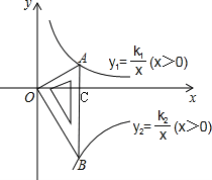
Rt△AOB中，∠B=30°，∠AOB=90°，

∴∠OAC=60°，

∵AB⊥OC，

∴∠ACO=90°，

∴∠AOC=30°，

设AC=a，则OA=2a，OC==a，

∴A(a，a)，

∵A在函数y1=（x＞0）的图象上，

∴k1=a×a=a2，

Rt△BOC中，OB=2OC=2a，

∴BC==3a，

∴B（a，-3a），

∵B在函数y2=（x＞0）的图象上，

∴k2=-3a×a=-3a2，

∴==-，

故答案为：-．