题目内容
【题目】如图，在正方形ABCD中，E，F分别为AB，AD上的点，且AE=AF，点M是EF的中点，连结CM.
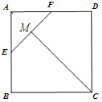
（1）求证：CM⊥EF.
（2）设正方形ABCD的边长为2，若五边形BCDEF的面积为
，请直接写出CM的长.
【答案】（1）见解析；（2）
【解析】
（1）连结 CE，CF，知道AE=AF，可得CE=CF，即可证明；（2）正方形ABCD的边长为2，若五边形BCDEF的面积为
，则可算出△AEF的面积，从而求出CM
（1）证明：连结 CE，CF
∵四边形 ABCD 是正方形
∴∠B=∠D=90°， BC=CD AB=AD
又 AE=AF
∴BE=DF
∴△CBE≌△CDF（SAS）
∴CE=CF
而M 是 EF 中点
∴CM⊥EF（等腰三角形三线合一）
（2）连接AM，由（1）可知，AMC三点共线，
正方形ABCD的边长为2，若五边形BCDEF的面积为，则△ AEF的面积为
，
则AC=
，AE=AF=
，
∴EF=
，AM=
，则CM=-=
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】数学成绩好的同学，其计算的准确性一定还可以，七年级某班数学李老师很注重学生的计算过关检测，在学完《有理数》后，对全班同学进行检测过关．下表是这个班的童威同学一周内五天检测过关成绩（以85分为标准，高出部分用“+”表示，低于的部分用“-”表示）
星期 | 一 | 二 | 三 | 四 | 五 |
分数变化 |
|
|
|
|
|
（1）本周内童威同学哪天的检测成绩最高？是多少？哪天的检测成绩最低？是多少？
（2）请计算这5次检测成绩的平均成绩是多少？
