题目内容
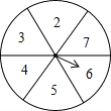
【题目】如图,现有一个均匀的转盘被平均分成六等份,分別标有2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转).
(1)转动转盘,转出的数字大于3的概率是______(直接填空);
(2)随机转动转盘,转盘停止后记下转出的数字,并与数字3和4分别为三条线段的长度,关于这三条线段:
①能构成三角形的概率是______(直接填空);
②能构成等腰三角形的概率是______(直接填空).
【答案】(1)![]() ,(2)①
,(2)①![]() ,②
,②![]() .
.
【解析】
(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4种,由概率公式可得;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成三角形的结果有5种,由概率公式可得;
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有2种,由概率公式可得.
解:(1)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,大于3的结果有4、5、6、7,共4种,
∴转出的数字大于3的概率是![]() =
=![]() ;
;
(2)①转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,并与数字3和4能够成三角形的结果有(2、3、4),(3、3、4),(4、3、4),(5、3、4),(6、3、4),共5种,
∴这三条线段能构成三角形的概率是![]() ;
;
②转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,能够成等腰三角形的结果有(3、3、4),(4、3、4),共2种,
∴这三条线段能构成等腰三角形的概率是![]() =
=![]() .
.
故答案为:![]() ,
,![]() ,
,![]() .
.

练习册系列答案
相关题目