题目内容
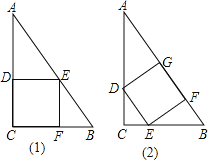
【题目】如图，在矩形ABCD中，E为AD中点，AC、BE交于F，连接DF，下列结论错误的是（ ）
A. CF=2AF B. BE⊥AC C. S△ABF = S△ADF D. S四边形CDEF = 5S△AEF
【答案】B
【解析】试题解析：∵四边形ABCD为矩形，
∴AD∥BC，AD=BC，
∵点E为AD的中点，
∴AE=
BC，
∵AE∥BC，
∴△AEF∽△CFB，
∴
，
∴FC=2AF,
故选项A正确；
选项B，无法得出；
由ΔAEF∽ΔBCF得，
SΔAEF:SΔCBF=1:4
∴SΔADF:SΔCBF=1:2
又SΔABC=
ABBC=
SΔBFC
∴SΔABF:SΔCBF=1:2
∴SΔADF= SΔABF,故选项C正确．
如图，过P作PH∥BE，交AC于点H.
∴AF=FH
∵CF=2AF
∴CH=HF
∴SΔADH=4SΔAEF
∵E是AD的中点
∴SΔDEF=SΔAEF
∴SΔDHF=2 SΔAEF
∵SΔDHF= SΔDHC
∴S四边形CDEF = 5S△AEF
故选B.
练习册系列答案
相关题目
