题目内容
【题目】如图,把矩形![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边的
边的![]() 处,若
处,若![]() ,
,![]() ,
,![]() ,则矩形
,则矩形![]() 的面积是________.
的面积是________.

【答案】![]()
【解析】
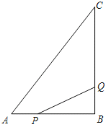
由把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,∠EFB=60°,易证得△EFB′是等边三角形,继而可得△A′B′E中,B′E=2A′E,则可求得B′E的长,然后由勾股定理求得A′B′的长,继而求得答案.
在矩形ABCD中, ∵AD∥BC, ∴∠DEF=∠EFB=60°,
∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,
∴∠EFB=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,
AE=A′E=2,AB=A′B′,
在△EFB′中, ∵∠DEF=∠EFB=∠EB′F=60° ∴△EFB′是等边三角形,
Rt△A′EB′中, ∵∠A′B′E=90°-60°=30°, ∴B′E=2A′E,而A′E=2,
∴B′E=4, ∴A′B′=2![]() , 即AB=2
, 即AB=2![]() , ∵AE=2,DE=6,
, ∵AE=2,DE=6,
∴AD=AE+DE=2+6=8, ∴矩形ABCD的面积=ABAD=2![]() ×8=16
×8=16![]() .故答案为:16
.故答案为:16![]() .
.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目