题目内容
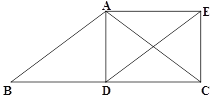
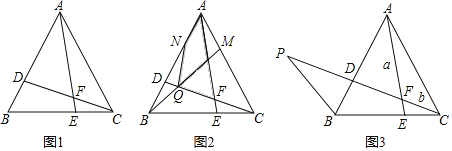
【题目】如图,点D,E分别在正△ABC的边AB,BC上,且BD=CE,CD,AE交于点F.
(1)①求证:△ACE≌△CBD;②求∠AFD的度数;
(2)如图2,若D,E,M,N分别是△ABC各边上的三等分点,BM,CD交于Q.若△ABC的面积为S,请用S表示四边形ANQF的面积 ;
(3)如图3,延长CD到点P,使∠BPD=30°,设AF=a,CF=b,请用含a,b的式子表示PC长,并说明理由.
【答案】(1)①见解析,②∠AFD=60°(2)![]() S;(3)PC=a+2b,见解析
S;(3)PC=a+2b,见解析
【解析】
(1)①由等边三角形的性质AB=AC=BC,∠ABC=∠ACE=∠BAC=60°,且BD=CE,可证△BDC≌△CEA;
②由三角形的外角性质可求∠AFD的度数;
(2)由等边三角形的性质可得BD=CE=AM=DN,且AB=AC=BC,∠ABC=∠ACE=∠BAC=60°,可证△ABM≌△CAE≌△BCD和△BDQ≌△CEF,由全等三角形的性质和三等分点性质,可求四边形ANQF的面积;
(3)在AC上截取AM=CE,由题意可证△BHC≌△CFA,可得BH=CF=b,AF=CH=a,∠PHB=60°,即可求PC的长.
证明:(1)①∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACE=∠BAC=60°,且BD=CE,
∴△BDC≌△CEA(SAS);
②∵△BDC≌△CEA,
∴∠CAE=∠BCD,
∵∠AFD=∠CAE+∠ACF=∠BCD+∠ACD=∠ACB,
∴∠AFD=60°;
(2)∵D,E,M,N分别是△ABC各边上的三等分点,
∴BD=CE=AM=DN,且AB=AC=BC,∠ABC=∠ACE=∠BAC=60°,
∴△ABM≌△CAE≌△BCD(SAS),
∴∠CAE=∠ABM=∠BCD,∠AMB=∠AEC=∠BDC,且BD=CE,
∴△BDQ≌△CEF(ASA),
∴S△BDQ=S△CEF,
∵BD=DN,
∴S△BDQ=S△DNQ=S△CEF,
∵D,E是AB,BC上三等分点,
∴S△BDC=S△CEA=![]() S△ABC=
S△ABC=![]() S,
S,
∵四边形ANQF的面积=S△ABC﹣S△AEC﹣S△DNQ﹣S四边形DFEB=S﹣![]() S﹣
S﹣![]() S,
S,
∴四边形ANQF的面积=![]() S,
S,
故答案为:![]() S;
S;
(3)PC=a+2b,
理由如下:如图,在AC上截取AM=CE,即AM=CE=BD,

∵AM=CE=BD,∠ABC=∠BAC=∠ACB=60°,AB=AC=CB,
∴△CBD≌△ACE≌△BAM(SAS),
∴∠CAE=∠BCD=∠ABM,且∠ABC=∠ACE,
∴∠MBC=∠ACD,且BC=AC,∠EAC=∠BCD,
∴△BHC≌△CFA(ASA),
∴BH=CF=b,AF=CH=a,
∵∠PHB=∠MBH+∠HCB=∠ABM+∠MBC=∠ABC,
∴∠PHB=60°,且∠BPD=30°,
∴∠PBH=90°,且∠BPH=30°,
∴PH=2BH=2b,
∴PC=PH+HC=a+2b.