题目内容
如图,AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.
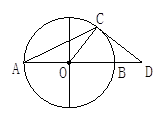
(1)CD与⊙O相切吗?如果相切,请你加以证明,如果不相切,请说明理由.
(2)若CD与⊙O相切,且∠D=30°,BD=8,求⊙O的半径.
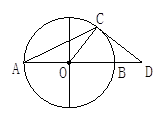
(1)CD与⊙O相切吗?如果相切,请你加以证明,如果不相切,请说明理由.
(2)若CD与⊙O相切,且∠D=30°,BD=8,求⊙O的半径.
(1)CD与⊙O相切.(2)⊙O的半径是8.
试题分析:解:(1)CD与⊙O相切.
理由:①C点在⊙O上(已知)
②∵AB是直径∴∠ACB=90°,即∠ACO+∠OCB=90°,
∵∠A=∠OCA且∠DCB=∠A,∴∠OCA=∠DCB, ∴∠OCD=90°.
综上:CD是⊙O的切线.
(2)在Rt△OCD中,∠D=30°,∴∠COD=60°,∴∠A=30°,∴∠BCD=30°.
∴BC=BD=8.∴AB=16,∴r=8. 答:(1)CD是⊙O的切线,(2)⊙O的半径是8.
点评:本题难度较大。主要考查学生圆的识点的学习。备考过程中,需将圆的相关知识联系记忆以及训练。

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
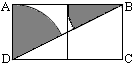








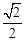



 的B处有一台风中心,该台风中心以每小时
的B处有一台风中心,该台风中心以每小时 的速度沿北偏东
的速度沿北偏东 的BD方向移动,在距离台风中心
的BD方向移动,在距离台风中心 内的地方都要受到其影响。
内的地方都要受到其影响。