题目内容
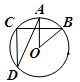
如图为圆柱形大型储油罐固定在U型槽上的横截面图.已知图中ABCD为等腰梯形(AB∥DC),支点A与B相距8m,罐底最低点到地面CD距离为1m.设油罐横截面圆心为O,半径为5m,∠D = 56°,求:(1)弧AB的度数(参考数据:sin53°≈0.8,tan56°≈1.5)
(2)U型槽的横截面(阴影部分)的面积.(参考数据:sin53°≈0.8,tan56°≈1.5,π≈3,结果保留整数)

(2)U型槽的横截面(阴影部分)的面积.(参考数据:sin53°≈0.8,tan56°≈1.5,π≈3,结果保留整数)

(1)106°;(2)20m2
试题分析:(1)连接AO、BO,过点A作AE⊥DC于点E,过点O作ON⊥DC于点N,ON交⊙O于点M,交AB于点F,则OF⊥AB.由OA =" OB" = 5m,AB = 8m,即可得到
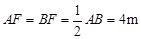 ,∠AOB = 2∠AOF.在Rt△AOF中,根据∠AOF的正弦函数即可求得∠AOF 的度数,从而求得结果;
,∠AOB = 2∠AOF.在Rt△AOF中,根据∠AOF的正弦函数即可求得∠AOF 的度数,从而求得结果;(2)先根据勾股定理求的OF,即可得到FN,再根据等腰梯形的性质可得AE =" FN" = 3m,DC =" AB" + 2DE.解Rt△ADE即可得到DE = 2m,DC = 12m,根据
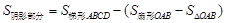 即可求得结果.
即可求得结果.(1)连接AO、BO,过点A作AE⊥DC于点E,过点O作ON⊥DC于点N,ON交⊙O于点M,交AB于点F,则OF⊥AB.
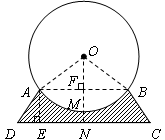
∵OA =" OB" = 5m,AB = 8m,
∴
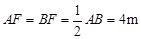 ,∠AOB = 2∠AOF.
,∠AOB = 2∠AOF.在Rt△AOF中,sin∠AOF =
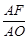 =" 0.8" = sin53°.
=" 0.8" = sin53°.∴∠AOF = 53°,则∠AOB = 106°.即弧AB度数为106°;
(2)∵
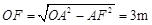 ,由题意得MN = 1m,
,由题意得MN = 1m,∴
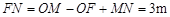 .
. ∵四边形ABCD是等腰梯形,AE⊥DC,FN⊥AB,
∴AE =" FN" = 3m,DC =" AB" + 2DE.
在Rt△ADE中,
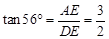 ,
,∴DE = 2m,DC = 12m.
∴
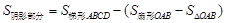
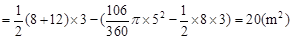
答:U型槽的横截面积约为20m2.
点评:根据题意作出辅助线,构造出直角三角形及等腰梯形,再利用勾股定理进行求解是解此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
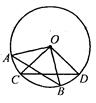
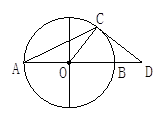

 ,过点T作AD延长线的垂线PQ,垂足为C。
,过点T作AD延长线的垂线PQ,垂足为C。
 ,求弦AD的长。
,求弦AD的长。