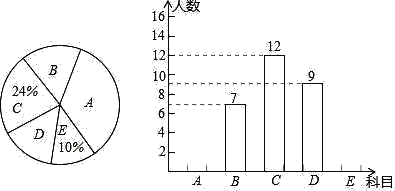
��Ŀ����
����Ŀ����ͼ��ʾ���ۿ�![]() λ�ڸۿ�
λ�ڸۿ�![]() ��������
��������![]() ������
����С��![]() λ�ڸۿ�
λ�ڸۿ�![]() ��ƫ��
��ƫ��![]() �ķ���һ���δ��Ӹۿ�
�ķ���һ���δ��Ӹۿ�![]() ��������
��������![]() ����ƫ��
����ƫ��![]() ����
����![]() ���ٶ�ʻ��ۿ�
���ٶ�ʻ��ۿ�![]() ��ͬʱһ�ҿ�ͧ�Ӹۿ�
��ͬʱһ�ҿ�ͧ�Ӹۿ�![]() �������ر�ƫ��
�������ر�ƫ��![]() �ķ�����
�ķ�����![]() ���ٶ�ʻ��С��
���ٶ�ʻ��С��![]() ����С��
������![]() ��
��![]() ��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��
��װ�������ʺ�������ԭ�����ٶȸ��δ���ȥ��
![]() ��ͧ�Ӹۿ�
��ͧ�Ӹۿ�![]() ��С��
��С��![]() ��Ҫ�ʱ�䣿
��Ҫ�ʱ�䣿
![]() ����ͧ��С��
����ͧ��С��![]() �����δ�����ǡ����ʱ
�����δ�����ǡ����ʱ![]() ����
����![]() ��ֵ����������ۿ�
��ֵ����������ۿ�![]() �ľ��룮
�ľ��룮
���𰸡�![]() ��ͧ�Ӹۿ�
��ͧ�Ӹۿ�![]() ��С��
��С��![]() ��ʱ��Ϊ
��ʱ��Ϊ![]() Сʱ��
Сʱ��![]() ��
��![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��������
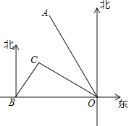
��1��Ҫ��B��C��ʱ�䣬��֪���ٶȣ���ֻҪ���BC��·�̣�������·�̹�ʽ������������ʱ�䣻
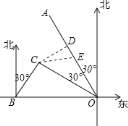
��2����C��CD��OA������ΪD������ᴦΪ��E�����OC=OBcos30��=60 ![]()
��CD= ![]() OC=30
OC=30 ![]() ��OD=OCcos30��=90����DE=90-3v����ֱ����CDE�����ù��ɶ����ó�CD2+DE2=CE2������303��2+��90-3v��2=602���ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
��OD=OCcos30��=90����DE=90-3v����ֱ����CDE�����ù��ɶ����ó�CD2+DE2=CE2������303��2+��90-3v��2=602���ⷽ�����v=20��40�����������������ۿ�O�ľ��룮
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
���ͧ�Ӹۿ�![]() ��С��
��С��![]() ��ʱ��Ϊ��
��ʱ��Ϊ��![]() ��Сʱ����
��Сʱ����
![]() ��
��![]() ��
��![]() ������Ϊ
������Ϊ![]() ������ᴦΪ��
������ᴦΪ��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ