题目内容
【题目】随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
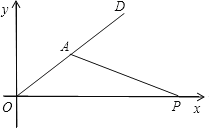
(1)填空:如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是 ;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能截住小球.
(参考数据:sin53°≈0.8,cos37°≈0.80,tan37°≈0.75,tan26.5°≈0.5)
【答案】(1)[2![]() ,45°] (2)见解析
,45°] (2)见解析
【解析】
试题分析:(1)作AB⊥x轴,由A点坐标可利用勾股定理求出OA的长及∠AOE的度数,再根据机器人的转动规则进行解答即可;
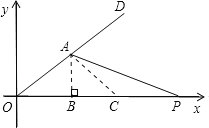
(2)作AC=PC,设PC=x,则BC=4﹣x,在Rt△ABC中利用勾股定理可求出x的值,再根据锐角三角函数的定义即可求出∠DAC的值,进而可得出答案.
解:(1)作AB⊥x轴,
∵A(2,2),
∴OA=![]() =2
=2![]() ,
,
∴∠AOB=45°,
∴给机器人发的指令为:[2![]() ,45°];
,45°];
(2)作AC=PC,由题意可知:PC=AC,设PC=x,则BC=4﹣x,
在Rt△ABC中:22+(4﹣x)2=x2,
得x=![]() ,
,
又∵tan∠BAC=![]() ,
,
∴∠BAC=37°,
∵∠OAB=45°,
∴∠OAC=37°+45°=82°,
∴∠DAC=180°﹣82°=98°,
∴输入的指令为[2.5,98°].

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目