题目内容
【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )
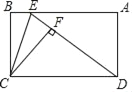
A. 6 B. 5 C. 4 D. 3
【答案】B
【解析】
先根据翻折变换的性质得出EF=BE=1,BC=CF=AD=3,可证得△AED≌△FDC 进而求得CD的长.
解:由题意得:E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,可得BE=EF=1,CF=BC=3,∠EFC=∠B=![]()
![]() ABCD为矩形,可得∠AED=∠CDF,
ABCD为矩形,可得∠AED=∠CDF,
在△AED与△FDC中有: AD=CF,∠A=∠DFC=![]() ,∠AED=∠CDF
,∠AED=∠CDF
![]() △AED≌△FDC,
△AED≌△FDC, ![]() ED=CD,
ED=CD,
设CD的长为x,在Rt△EAD中,
有![]() ,
,
即:![]() ,解得;x=5,
,解得;x=5,
故答案为:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目