题目内容
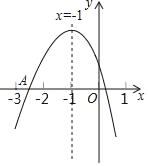
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,下列结论中:
①abc<0;②9a﹣3b+c<0;③b2﹣4ac>0;④a>b,
正确的结论是_____(只填序号)
【答案】②③④
【解析】
运用二次函数的图形与性质进行判断即可.
解析:①因为抛物线开口向下,所以a<0.因为抛物线的对称轴为直线x=-1<0, b<0,因为抛物线与y轴的交点在y轴正半轴上,所以c>0.所以abc>0.故①错误;
②因为由图像得当x=一3时,y<0,所以9a-3b+c<0.故②正确;
③因为图像与z轴有两个交点,所以b2﹣4ac>0.故③正确;
④因为抛物线的对称轴为直线x=-1,![]() ,b=2a
,b=2a
所以a-b=a-2a=-a>0,所以a>b.故④正确.
故正确的有②③④,
故答案:②③④.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】某超市第一次用![]() 元购进甲、乙两种商品,其中甲商品件数的
元购进甲、乙两种商品,其中甲商品件数的![]() 倍比乙商品件数的
倍比乙商品件数的![]() 倍多
倍多![]() 件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
甲 | 乙 | |
进价(元/件) | 20 | 28 |
售价(元/件) | 26 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、 乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的![]() 倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多
倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多![]() 元,则第二次乙商品是按原价打几折销售的?
元,则第二次乙商品是按原价打几折销售的?