��Ŀ����
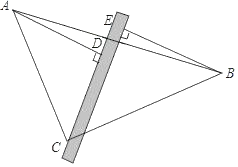
����Ŀ����֪�����ϵ�A��ʾ����Ϊ6��B��������������һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵĶ����������������˶������˶�ʱ��Ϊt![]() �롣
�롣
![]()
��1�������ϵ�B��ʾ������______������P�˶���AB���е�ʱ��������ʾ������_____��
��2������Q�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Qͬʱ��������
�ٵ���P�˶�������ʱ����P�ϵ�Q��
�ڵ���P�˶�������ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
���𰸡���1��-4��1��2���ٵ���P�˶�2.5��ʱ����P�ϵ�Q���ڵ���P�˶�0.5���4.5��ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
��������
(1)����֪��OA=6����OB=AB-OA=4��д�������ϵ�B����ʾ���������ݵ�P�˶���AB���е㣬���ɵó�P������ʾ����:
��2�������P�˶�t��ʱ�ϵ�Q�����ݵ�����ϵ�õ�6t-2t=10��Ȼ����⼴�ɣ�
�ڷֵ�Pδ������Q�͵�P������Q����������ۣ����˶�ʱ��Ϊm����������õ���P������Q����6-6m ��-��-4-2m��=8����P����Q����-4-2m��-��6-6m ��=8����⼴�ɣ�
�⣺��1���������ϵ�A��ʾ����Ϊ6��
��OA=6��
��OB=AB-OA=10-6=4��
��B��ԭ����ߣ�
�������ϵ�B����ʾ����Ϊ-4��
�������ϵ�A��ʾ����Ϊ6�������ϵ�B����ʾ����Ϊ-4
��AB���е��ǣ�1
�������ϵ�P����ʾ����Ϊ��1
�ʴ�Ϊ��-4��1
��2�������P�˶�t��ʱ�ϵ�Q��
��6t-2t=10��
���t=2.5��
���Ե���P�˶�2.5��ʱ����P�ϵ�Q��
���赱��P�˶�m��ʱ����P���Q��ľ���Ϊ8����λ���ȣ������ϵ�P����ʾ����Ϊ��6-6m�������ϵ�Q����ʾ����Ϊ��-4-2m��
��P������Q����6-6m ��-��-4-2m��=8�����m=0.5��
��P����Q����-4-2m��-��6-6m ��=8�����m=4.5��
���Ե���P�˶�0.5���4.5��ʱ����P���Q��ľ���Ϊ8����λ���ȣ�

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�