题目内容
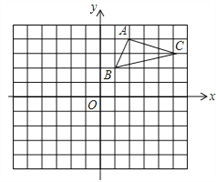
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标A1 ________________.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标A2__________________.
(3) △ABC是否为直角三角形?答_________(填是或者不是).
(4)利用格点图,画出BC边上的高AD,并求出AD的长,AD=_____________.
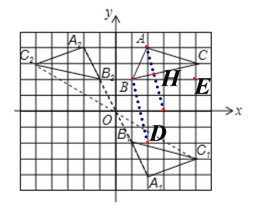
【答案】 (2.-4) (-2,4) 不是 ![]()
【解析】试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,即△A2B2C2与△A1B1C1关于点O成中心对称,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2;
(3)根据勾股定理逆定理解答即可;
(4)连接BD,过点A作AH∥BD交BC与点H,然后利用面积法求AH的长度即可.
解:(1)如图所示:点A1的坐标(2,-4);
(2)如图所示,点A2的坐标(-2,4);
(3)∵AC2=32+12=10, AB2=22+12=5, BC2=42+12=17,
∴AC2+ AB2≠ BC2,
∴△ABC不是直角三角形;
(4)连接BD,过点A作AH∥BD交BC与点H.
∵BB1=BE, ∠BB1D=∠BEC,B1D=CE,
∴△BB1D=△BEC,
∴∠CBE=∠DBB1.
∵∠DBE=∠DBB1=90°,
∴∠DBE=∠CBE =90°,
∴BD⊥BC,
∴AH⊥BC.
∵BC2=42+12=17,
∴BC=![]() .
.
∵S△ABC=4×2-![]() ×2×1-
×2×1-![]() ×3×1-
×3×1-![]() ×4×1=
×4×1=![]() ,
,
∴![]() BC·AH=
BC·AH=![]() ,
,
∴![]() AH=7,
AH=7,
∴AH= ![]() .
.

【题目】八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | a | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
请解答以下问题:
(1)频数分布表中a= ,把频数分布直方图补充完整;
(2)求该居委会用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该居委会有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?

【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?