题目内容
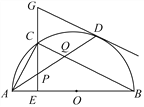
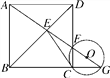
【题目】如图,由正方形ABCD的顶点A引一直线分别交BD、CD及BC的延长线于E、F、G,连接EC.
求证:CE是△CGF的外接圆⊙O的切线.
【答案】 详见解析.
【解析】试题分析:通过全等三角形的判定定理SAS判定△ABE≌△CBE,然后根据全等三角形的对应角相等知∠BAE=∠BCE,由∠BAE+∠G=90°,得出∠BCE+∠OCG=90°,从而∠ECO=90°,进而就可求得EC是△CGF的外接圆⊙O的切线..
证明:如图,连接OC,则OG=OC,
∴∠G=∠OCG.
∵四边形ABCD是正方形,
∴AB=CB,∠ABE=∠CBE=45°.
又∵BE=BE,
∴△ABE≌△CBE(SAS),
∴∠BAE=∠BCE.
∵∠BAE+∠G=90°,
∴∠BCE+∠OCG=90°,
∴∠ECO=90°,
∴EC是△CGF的外接圆⊙O的切线.

练习册系列答案
相关题目