题目内容
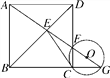
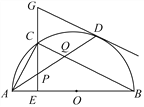
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
【答案】②③
【解析】试题分析:∠BAD与∠ABC不一定相等,选项①错误;
∵GD为圆O的切线,∴∠GDP=∠ABD,又AB为圆O的直径,∴∠ADB=90°,∵CF⊥AB,∴∠AEP=90°,∴∠ADB=∠AEP,又∠PAE=∠BAD,∴△APE∽△ABD,∴∠ABD=∠APE,又∠APE=∠GPD,∴∠GDP=∠GPD,∴GP=GD,选项②正确;
由AB是直径,则∠ACQ=90°,如果能说明P是斜边AQ的中点,那么P也就是这个直角三角形外接圆的圆心了.Rt△BQD中,∠BQD=90°-∠6, Rt△BCE中,∠8=90°-∠5,而∠7=∠BQD,∠6=∠5, 所以∠8=∠7, 所以CP=QP;由②知:∠3=∠5=∠4,则AP=CP; 所以AP=CP=QP,则点P是△ACQ的外心,选项③正确.
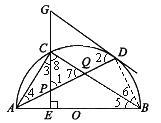
则正确的选项序号有②③.故答案为:②③.

练习册系列答案
相关题目