题目内容
【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
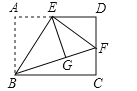
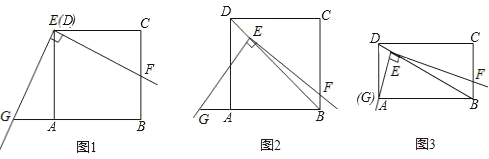
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求![]() 的值.
的值.
【答案】(1)详见解析;(2)=;(3)![]() .
.
【解析】试题分析:(1)证明△EAG≌△ECF即可得出结论;
(2)过点E作EM⊥AB于点M,作EN⊥BC于点N,由(1)同理证出△EMG≌△ENF得出结论;
(3)过点E作EM⊥AB于点M,作EN⊥BC于点N,由(2)得出经验,证得结论则需要通过由平行线得出比例式和两三角形相似得出比例式来解决.
试题解析:(1)证明:∵∠AEF+∠AEG=90°,∠AEF+∠CEF=90°,
∴∠AEG=∠CEF,
又∵∠GAE=∠C=90°,EA=EC,
∴△EAG≌△ECF(ASA)
∴EG=EF
(2)EF=EG;
过点E作EM⊥AB于点M,作EN⊥BC于点N,如图2所示,
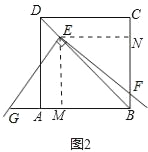
则∠MEN=90°,EM=EN,
∴∠GEM=∠FEN,
又因为∠EMG=∠ENF=90°,
∴△EMG≌△ENF
∴EF=EG.
故答案为:=.
(3)过点E作EM⊥AB于点M,作EN⊥BC于点N,如图3所示:
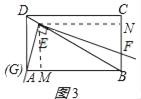
则∠MEN=90°,EM∥BC,EN∥AB,
∴![]() ,
,
∴![]() ,
,
又∵∠GEM+∠MEF=90°,∠FEN+∠MEF=90°,
∴∠FEN=∠GEM,
∴Rt△GME∽Rt△FNE,
∴![]() .
.

【题目】李林想了解班上同学是否具有阅读习惯及分享意识,于是设计了一份调查问卷:

李林对班上![]() 位同学进行了调查,收集调查结果如下:
位同学进行了调查,收集调查结果如下:
问题1的调查结果
选项 |
|
|
|
人数 |
|
|
|
问题2的调查结果
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 请在下图中将问题1的调查结果用条形统计图表示出来:
请在下图中将问题1的调查结果用条形统计图表示出来:

![]() 请用下面的统计表整理问题2的调查结果:
请用下面的统计表整理问题2的调查结果:
选项 | 划记 | 人数 | 百分比 |
| |||
| |||
| |||
合计 |
![]() 根据调查结果,你认为班上同学在阅读习惯及分享意识方面做得怎么样?
根据调查结果,你认为班上同学在阅读习惯及分享意识方面做得怎么样?