题目内容
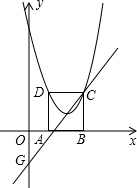
如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=2
,直线y=
x-2
经过点C,交y轴于点G.
(1)点C、D的坐标;
(2)求顶点在直线y=
x-2
上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=
x-2
平移,平移后的抛物线交y轴于点F,顶点为点E.平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线的解析式;若不存在,请明理由.
| 3 |
| 3 |
| 3 |
(1)点C、D的坐标;
(2)求顶点在直线y=
| 3 |
| 3 |
(3)将(2)中的抛物线沿直线y=
| 3 |
| 3 |

(1)令y=2
,2
=
x-2
,解得x=4,则OA=4-3=1,
∴C(4,2
),D(1,2
);
(2)由二次函数对称性得,顶点横坐标为
=
,
令x=
,则y=
×
-2
=
,
∴顶点坐标为(
,
),
∴设抛物线解析式为y=a(x-
)2+
,把点D(1,2
)代入得,a=
,
∴解析式为y=
(x-
)2+
;
(3)设顶点E在直线上运动的横坐标为m,则E(m,
m-2
)(m>0)
∴可设解析式为y=
(x-m)2+
m-2
,
①当FG=EG时,FG=EG=2m,则F(0,2m-2
),代入解析式得:
m2+
m-2
=2m-2
,
得m=0(舍去),m=
-
,
此时所求的解析式为:y=
(x-
+
)2+3-
;
②当GE=EF时,FG=2
m,则F(0,2
m-2
),
代入解析式得:
m2+
m-2
=2
m-2
,解得m=0(舍去),m=
,
此时所求的解析式为:y=
(x-
)2-
;
③当FG=FE时,不存在.
| 3 |
| 3 |
| 3 |
| 3 |
∴C(4,2
| 3 |
| 3 |
(2)由二次函数对称性得,顶点横坐标为
| 1+4 |
| 2 |
| 5 |
| 2 |
令x=
| 5 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
| ||
| 2 |
∴顶点坐标为(
| 5 |
| 2 |
| ||
| 2 |
∴设抛物线解析式为y=a(x-
| 5 |
| 2 |
| ||
| 2 |
| 3 |
2
| ||
| 3 |
∴解析式为y=
2
| ||
| 3 |
| 5 |
| 2 |
| ||
| 2 |
(3)设顶点E在直线上运动的横坐标为m,则E(m,
| 3 |
| 3 |
∴可设解析式为y=
2
| ||
| 3 |
| 3 |
| 3 |
①当FG=EG时,FG=EG=2m,则F(0,2m-2
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
得m=0(舍去),m=
| 3 |
| 3 |
| 2 |
此时所求的解析式为:y=
2
| ||
| 3 |
| 3 |
| 3 |
| 2 |
7
| ||
| 2 |
②当GE=EF时,FG=2
| 3 |
| 3 |
| 3 |
代入解析式得:
2
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
此时所求的解析式为:y=
2
| ||
| 3 |
| 3 |
| 2 |
| ||
| 2 |
③当FG=FE时,不存在.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目



 份x(月)满足的函数关系如图所示.
份x(月)满足的函数关系如图所示.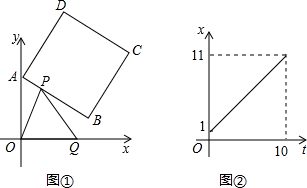 能,写出所有符合条件的t的值;若不能,请说明理由.
能,写出所有符合条件的t的值;若不能,请说明理由.
