题目内容
正方形ABCD的边长为2,E是射线CD上的动点(不与点D重合),直线AE交直线BC于点G,∠BAE的平分线交射线BC于点O.
(1)如图,当CE=
时,求线段BG的长;
(2)当点O在线段BC上时,设
=x,BO=y,求y关于x的函数解析式;
(3)当CE=2ED时,求线段BO的长.

(1)如图,当CE=
| 2 |
| 3 |
(2)当点O在线段BC上时,设
| CE |
| ED |
(3)当CE=2ED时,求线段BO的长.

(1)在边长为2的正方形ABCD中,CE=
,得DE=CD-CE=2-
=
,
又∵AD∥BC,即AD∥CG,
∴
=
=
,
得CG=1.
∵BC=2,
∴BG=3;
(2)当点O在线段BC上时,过点O作OF⊥AG,垂足为点F.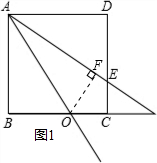
∵AO为∠BAE的角平分线,∠ABO=90°,
∴OF=BO=y.
在正方形ABCD中,AD∥BC,
∴
=
=x.
∵AD=2,
∴CG=2x.
又∵
=x,CE+ED=2,
∴得CE=
.
∵在Rt△ABG中,AB=2,BG=2+2x,∠B=90°,
∴AG=2
.
∵AF=AB=2,
∴FG=AG-AF=2
-2.
∵
=
,
即y=
•FG,
得y=
.(x≥0);
(3)当CE=2ED时,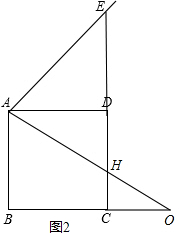
①当点O在线段BC上时如图(1),即x=2,由(2)得OB=y=
;
②当点O在线段BC延长线上时,如图(2),CE=2DE=4,ED=2,在Rt△ADE中,AE=2
.
设AO交线段DC于点H,
∵AO是∠BAE的平分线,
∴∠BAH=∠HAE,
又∵AB∥CD,
∴∠BAH=∠AHE.
∴∠HAE=∠AHE.
∴EH=AE=2
.
∴CH=4-2
,
∵AB∥CD,
∴
=
,
∴
=
,得BO=2
+2.
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
又∵AD∥BC,即AD∥CG,
∴
| CG |
| AD |
| CE |
| DE |
| 1 |
| 2 |
得CG=1.
∵BC=2,
∴BG=3;
(2)当点O在线段BC上时,过点O作OF⊥AG,垂足为点F.

∵AO为∠BAE的角平分线,∠ABO=90°,
∴OF=BO=y.
在正方形ABCD中,AD∥BC,
∴
| CG |
| AD |
| CE |
| ED |
∵AD=2,
∴CG=2x.
又∵
| CE |
| ED |
∴得CE=
| 2x |
| 1+x |
∵在Rt△ABG中,AB=2,BG=2+2x,∠B=90°,
∴AG=2
| x2+2x+2 |
∵AF=AB=2,
∴FG=AG-AF=2
| x2+2x+2 |
∵
| OF |
| FG |
| AB |
| BG |
即y=
| AB |
| BG |
得y=
2
| ||
| x+1 |
(3)当CE=2ED时,

①当点O在线段BC上时如图(1),即x=2,由(2)得OB=y=
2
| ||
| 3 |
②当点O在线段BC延长线上时,如图(2),CE=2DE=4,ED=2,在Rt△ADE中,AE=2
| 2 |
设AO交线段DC于点H,
∵AO是∠BAE的平分线,
∴∠BAH=∠HAE,
又∵AB∥CD,
∴∠BAH=∠AHE.
∴∠HAE=∠AHE.
∴EH=AE=2
| 2 |
∴CH=4-2
| 2 |
∵AB∥CD,
∴
| CH |
| AB |
| CO |
| BO |
∴
4-2
| ||
| 2 |
| BO-2 |
| BO |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目