题目内容
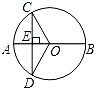
已知:⊙O的半径为5,AB为直径,CD为弦,CD⊥AB于E,若CD=6,求AE的长.
如图,连接OC;
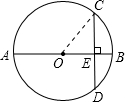
∵AB⊥CD
∴CE=
CD=3
在Rt△COE中,OE=
=
=4
∴AE=OA+OE=5+4=9.
如图,连接OC;
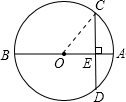
∵AB⊥CD
∴CE=
CD=3,
在Rt△COE中,OE=
=
=4
∴AE=OA-OE=5-4=1.
∴AE的长为9或1.

∵AB⊥CD
∴CE=
| 1 |
| 2 |
在Rt△COE中,OE=
| OC2-CE2 |
| 52-32 |
∴AE=OA+OE=5+4=9.
如图,连接OC;

∵AB⊥CD
∴CE=
| 1 |
| 2 |
在Rt△COE中,OE=
| OC2-CE2 |
| 52-32 |
∴AE=OA-OE=5-4=1.
∴AE的长为9或1.

练习册系列答案
相关题目